Nov 7, 2018

排序算法知多少

大学里学的第一门编程语言是 c++，c++ 的课程中接触的第一种排序算法是冒泡排序，这已经过去八年，很惭愧的是到目前只了解冒泡排序和插入排序两种，作为一名合格的程序猿也应该了解了解其它的排序算法吧！所以开本文记录整理网上所谓的十大排序算法。

2018111115418975029904.gif

排序算法概述

网上常见的排序算法有十种：冒泡排序、快速排序、插入排序、希尔排序、选择排序、堆排序、归并排序、计数排序、基数排序、桶排序。

排序算法分类

上面十大排序算法按照非线性时间比较类排序^[非线性时间比较类排序: 通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 $O(n\log n)$ ，因此称为非线性时间比较类排序。]和线性时间非比较类排序^[线性时间非比较类排序: 不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。]进行分类：

![](https://pichome-1254392422.cos.ap-chengdu.myqcloud.com/blog/img/Surface Pro 4 – 1@2x.png)

排序算法对比

从时间复杂度^[时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。]、空间复杂度^[空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。]和 稳定性^[稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。]三方面对比十种排序方法如下：

排序算法 时间复杂度(平均) 时间复杂度(最坏) 时间复杂度(最好) 空间复杂度(平均) 稳定性
冒泡排序 $O(n^2)$ $O(n^2)$ $O(n)$ $O(1)$ 稳定
快速排序 $O(n\log_2 n)$ $O(n^2)$ $O(n\log_2 n)$ $O(n\log_2 n)$ 不稳定
插入排序 $O(n^2)$ $O(n^2)$ $O(n)$ $O(1)$ 稳定
希尔排序 $O(n^{1.3})$ $O(n^2)$ $O(n)$ $O(1)$ 不稳定
选择排序 $O(n^2)$ $O(n^2)$ $O(n^2)$ $O(1)$ 不稳定
堆排序 $O(n\log_2 n)$ $O(n\log_2 n)$ $O(n\log_2 n)$ $O(1)$ 不稳定
归并排序 $O(n\log_2 n)$ $O(n\log_2 n)$ $O(n\log_2 n)$ $O(n)$ 稳定
计数排序 $O(n+k)$ $O(n+k)$ $O(n+k)$ $O(n+k)$ 稳定
基数排序 $O(n+k)$ $O(n^2)$ $O(n)$ $O(n+k)$ 稳定
桶排序 $O(n\cdot k)$ $O(n \cdot k)$ $O(n \cdot k)$ $O(n+k)$ 稳定

冒泡排序

2018年11月08日

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作重复地进行直到没有元素需要交换，即排序完成。这个算法进行时越小的元素会经交换慢慢“浮”到数列的顶端，故得“冒泡之名。

冒泡排序步骤

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较为止。

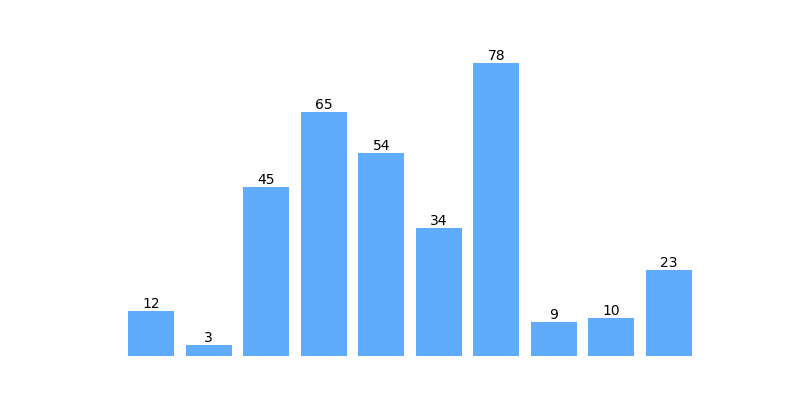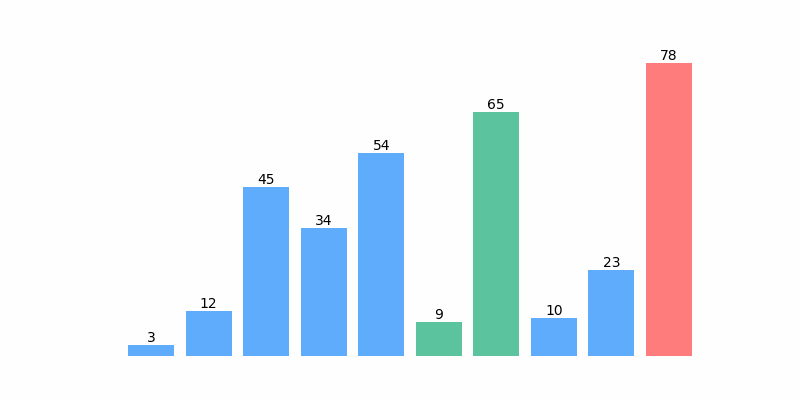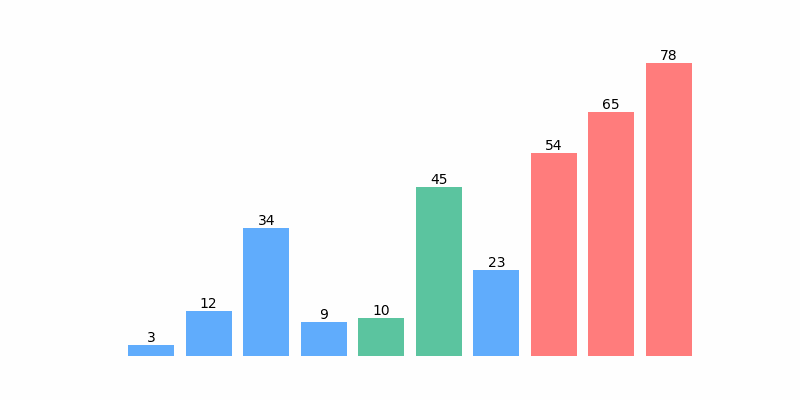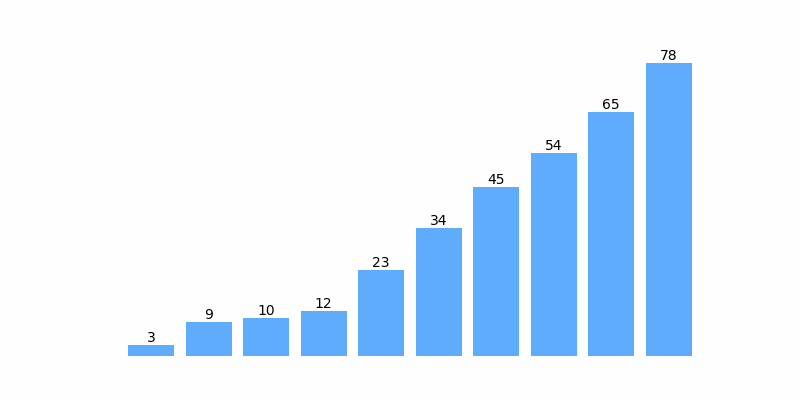
为了方便理解，以数组 [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23] 排序为例，排序过程如以下动图：

2018111115418975029904.gif

冒泡排序示例代码

python3 实现冒泡算法封装成函数如下：

def bubble_sort(numlist):
    length = len(numlist)
    for i in range(length - 1):
        for j in range(length -1 - i):
            if numlist[j] > numlist[j + 1]:
                numlist[j], numlist[j + 1] = numlist[j + 1], numlist[j]
    return numlist

进行测试，简单测试代码如下：

if __name__ == '__main__':
    l = [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23]
    print(f'sorting... {l}')
    l = bubble_sort(l)
    print(f'sorted  -> {l}')

运行脚本，一切OK：

$ python3 bubble.py
sorting... [12, 3, 45, 65, 54, 34, 78, 9, 10, 23]
sorted  -> [3, 9, 10, 12, 23, 34, 45, 54, 65, 78]

快速排序

2018年11月09日

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔提出。在平均状况下，排序 $n$ 个项目要 $O(n\log n)$（大O符号）次比较。在最坏状况下则需要 $O(n^2)$ 次比较，但这种状况并不常见。事实上，快速排序 $\Theta (n\log n)$ 通常明显比其他算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成。

快速排序步骤

快排采用和归并排序相同的分而治之的思想，将待排序数组分成左右两个子数组，对两部分子数组独立排序。当子数组均有序时，整个数组也就有序了^[Python实现快排及其可视化——快排基本原理]。

  1. 将原始数组 data 随机打乱，以消除对输入的依赖（本步可选）
  2. 选择数组的某个元素作切分元素 v，比如首个元素 data[0]
  3. 切分数组
    • 从左往右找到第一个大于切分元素v的元素 data[i]
    • 从右到左找到第一个小于切分元素v的元素 data[j]
    • 交换 data[i] 与 data[j]
    • 重复以上三步直到 i >= j
    • 交换 data[j] 与切分元素 data[0]
  4. 递归调用，对切分后的左侧子数组进行排序
  5. 递归调用，对切分后的右侧子数组进行排序

为了方便理解，以数组 [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23] 排序为例，排序过程如以下动图:

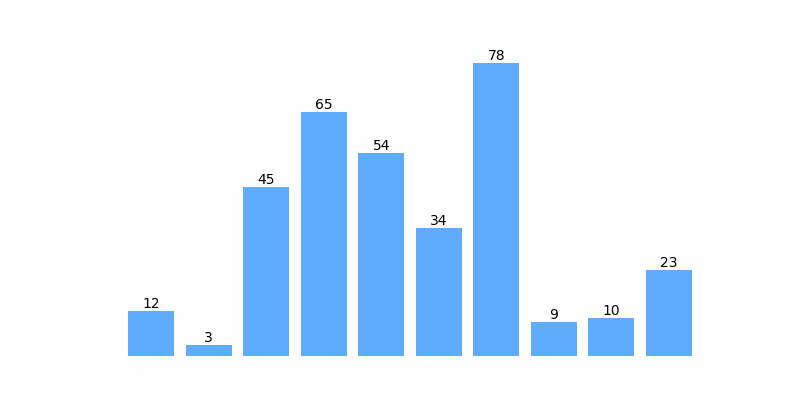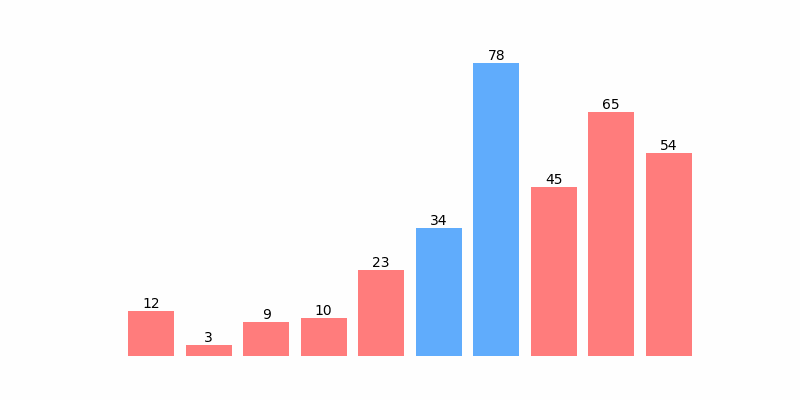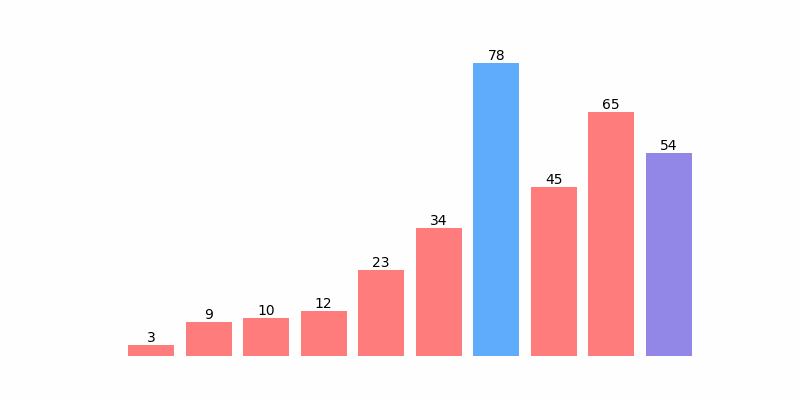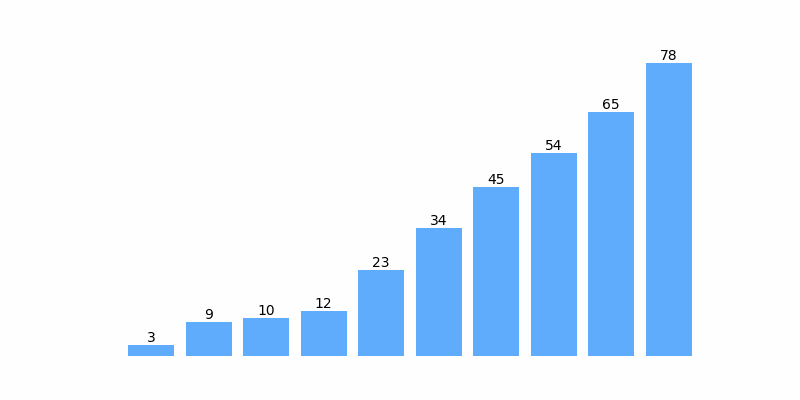
20181111154194773939997.gif

快速排序示例代码

python3 实现快速排序封装成函数如下(代码中选择最后一个元素作切分元素 v)：

    if lo < hi:
        p = partition(data, lo, hi)
        quicksort(data, lo, p)
        quicksort(data, p+1, hi)
    return

def partition(data, lo, hi):
    pivot = data[hi-1]
    i = lo - 1
    for j in range(lo, hi):
        if data[j] < pivot:
            i += 1
            data[i], data[j] = data[j], data[i]
    if data[hi-1] < data[i+1]:
        data[i+1], data[hi-1] = data[hi-1], data[i+1]
    return i+1

测试实现的快速排序算法：

if __name__ == '__main__':
    l = [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23]
    print(f'sorting... {l}')
    quicksort(l, 0, len(l))
    print(f'sorted:    {l}')

测试一下：

$ python3 quick.py
sorting... [12, 3, 45, 65, 54, 34, 78, 9, 10, 23]
sorted:    [3, 9, 10, 12, 23, 34, 45, 54, 65, 78]

插入排序

2018年11月10日

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用 in-place 排序（即只需用到 $O(1)$ 的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

插入排序步骤

一般来说，插入排序都采用 in-place 在数组上实现。具体算法描述如下：

  1. 从第一个元素开始，该元素可以认为已经被排序
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
  4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤2~5

为了方便理解，以数组 [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23] 排序为例，排序过程如以下动图：

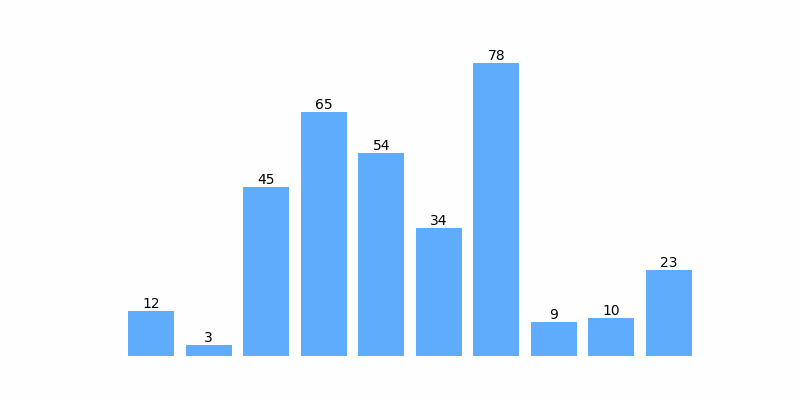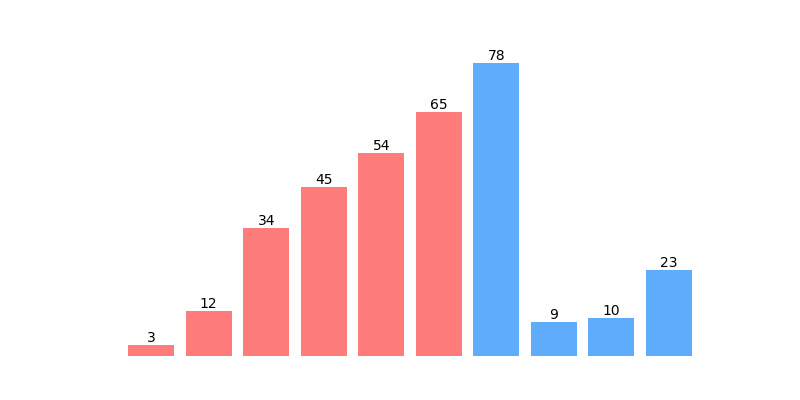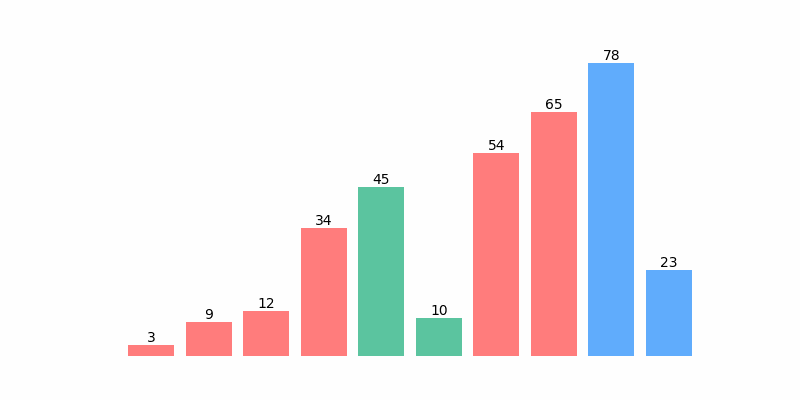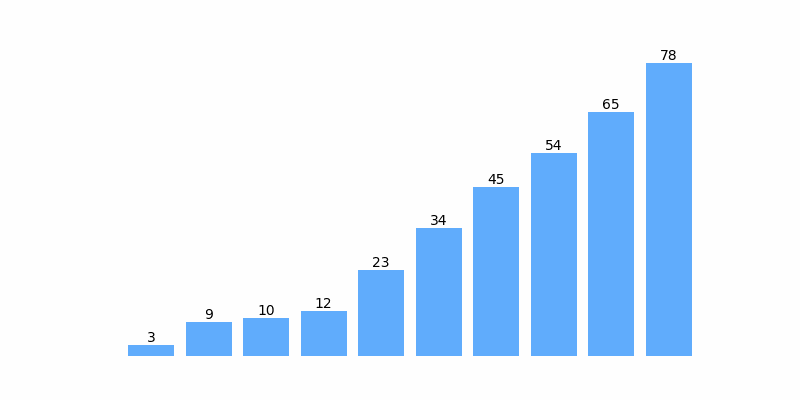
20181111154194998895578.gif

插入排序示例代码

def insert_sort(data):
    n = len(data)
    if n == 1:
        return data
    for i in range(1, n):
        for j in range(i, 0, -1):
            if data[j] < data[j-1]:
                data[j], data[j-1] = data[j-1], data[j]
            else:
                break
    return data

测试一下：

if __name__ == '__main__':
    l = [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23]
    print(f'sorting... {l}')
    l = insert_sort(l)
    print(f'sorted:    {l}')

结果：

$ python3 insert.py
sorting... [12, 3, 45, 65, 54, 34, 78, 9, 10, 23]
sorted:    [3, 9, 10, 12, 23, 34, 45, 54, 65, 78]

希尔排序

2018年11月11日

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布。希尔排序是非稳定排序算法。希尔排序是基于插入排序的以下两点性质而提出改进方法的：

  1. 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
  2. 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为普通插入排序，这就保证了数据一定会被排序。

Donald Shell最初建议步长选择为 $\frac{n}{2}$ 并且对步长取半直到步长达到1。虽然这样取可以比 $\mathcal {O} (n^{2})$ 类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。比如，如果一个数列以步长5进行了排序然后再以步长3进行排序，那么该数列不仅是以步长3有序，而且是以步长5有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就不会以如此短的时间完成排序了^[已知的最好步长序列是由 Sedgewick 提出的 (1, 5, 19, 41, 109,...)，该序列的项来自 $9\times 4^{i}-9\times 2^{i}+1 $ 和 $2^{{i+2}}\times (2^{{i+2}}-3)+1$ 这两个算式。这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。”用这样步长序列的希尔排序比插入排序要快，甚至在小数组中比快速排序和堆排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。——希尔排序 @ 维基百科 ]。

希尔排序步骤

这里步长选择为 $\frac{n}{2}$ 并且对步长取半直到步长达到1的序列：

序列个数为 $n$，初始化步长 $stepsize = n$。

  1. 取新步长为 $\frac{stepsize}{2}$，如果 $stepsize < 1$ 算法结束
  2. 从第一个元素开始，该元素可以认为已经被排序
  3. 取出按照新步长 $stepsize$ 的下一个元素，在已经排序的元素序列中从后向前扫描
  4. 如果该元素（已排序）大于新元素，将该元素移到按新步长的下一位置
  5. 重复步骤 4，直到找到已排序的元素小于或者等于新元素的位置
  6. 将新元素插入到该位置
  7. 重复步骤 3~6，直到按照新步长 $stepsize$ 的插入排序结束
  8. 重复 1～7步骤

为了方便理解，以数组 [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23] 排序为例，排序过程如以下动图：

20181112154195404360778.gif

希尔排序示例代码

def shell_sort(numlist):
    n = len(numlist)
    # 初始步长
    stepsize = n // 2
    while stepsize > 0:
        for i in range(stepsize, n):
            # 每个步长进行插入排序
            temp = numlist[i]
            j = i
            # 插入排序
            while j >= stepsize and numlist[j - stepsize] > temp:
                numlist[j] = numlist[j - stepsize]
                j -= stepsize
            numlist[j] = temp
        # 得到新的步长
        stepsize = stepsize // 2
    return numlist

测试一下：

if __name__ == '__main__':
    l = [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23]
    print(f'sorting... {l}')
    l = shell_sort(l)
    print(f'sorted:    {l}')

结果：

$ python3 shell.py
sorting... [12, 3, 45, 65, 54, 34, 78, 9, 10, 23]
sorted:    [3, 9, 10, 12, 23, 34, 45, 54, 65, 78]

选择排序

2018年11月12日

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 $n$ 个元素的表进行排序总共进行至多 $n-1$ 次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

选择排序步骤

  1. 选择未排序的序的首元素作为作为比对元素
  2. 往后进行比较，找到最小的元素与首位的元素互换位置
  3. 重复 1～2 步一直到只剩一个序列

为了方便理解，这里以对序列 [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23] 排序为例展示排序过程动画如下：

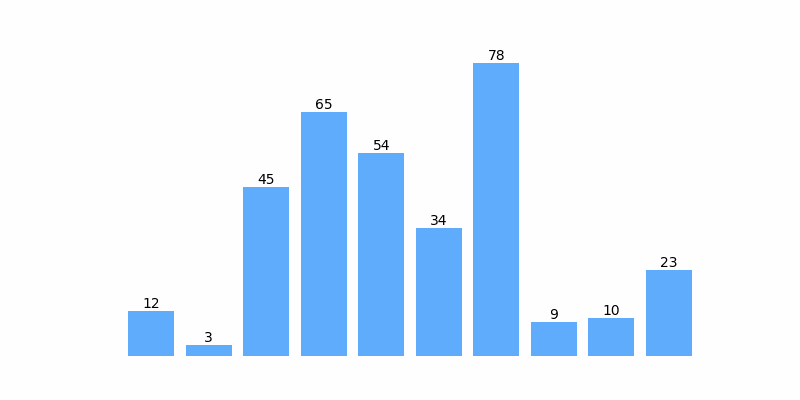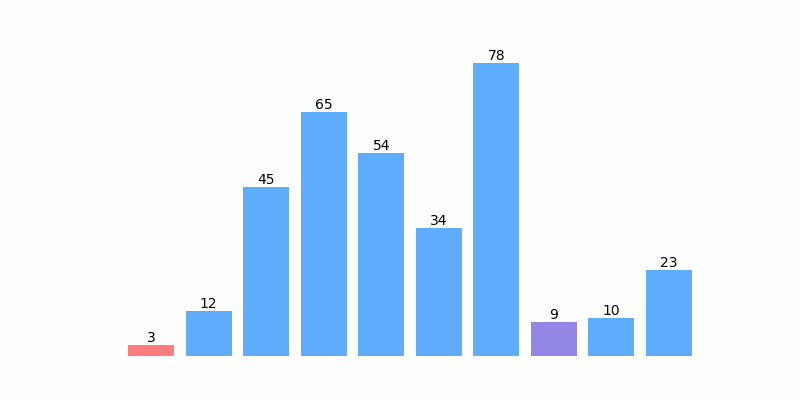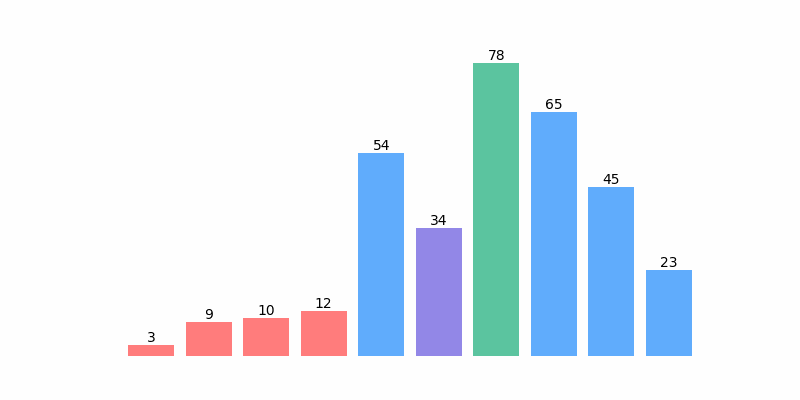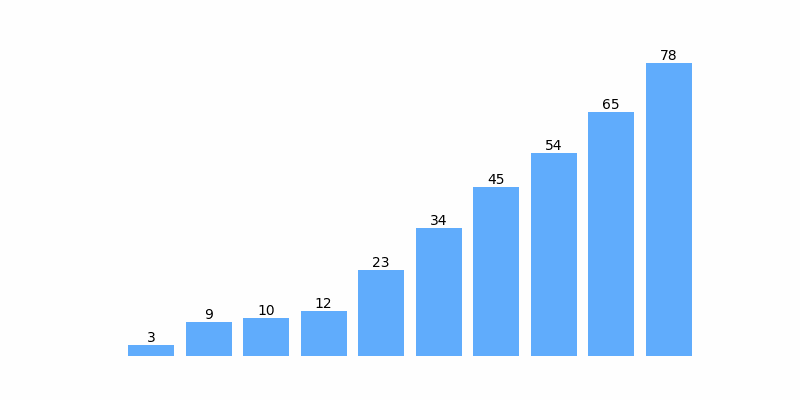
20181112154200663696412.gif

选择排序示例代码

def select_sort(numlist):
    length = len(numlist)
    for i in range(length-1):
        min_index = i
        for j in range(i+1, length):
            if numlist[min_index] > numlist[j]:
                min_index = j
        if min_index != i:
            numlist[min_index], numlist[i] = numlist[i], numlist[min_index]
    return numlist

测试一下封装的算法：

if __name__ == '__main__':
    l = [12, 3, 45, 65, 54, 34, 78, 9 ,10, 23]
    print(f'sorting... {l}')
    print(f'sorrted    {select_sort(l)}')

测试结果：

$ python3 select.py
sorting... [12, 3, 45, 65, 54, 34, 78, 9, 10, 23]
sorrted    [3, 9, 10, 12, 23, 34, 45, 54, 65, 78]

堆排序

归并排序

计数排序

基数排序

桶排序

未完待续。。。

访问量