《雷神之锤》丧心病狂的平方根倒数速算法
今天学习《Python科学计算》,看到了一个绝对丧心病狂、计算速度碾压标准sqrt库函数的平方根倒数速算法,据说平均比标准库的sqrt快4倍。这个算法是约翰-卡马克(John Carmack)创造的,据说他是一个伟大的3D引擎开发者,《雷神之锤3》用的就是他开发的3D引擎。
贴出代码 1/sqrt(number) :
float Q_sqrt( float number ) {
long i;
float x2, y;
const float threeHalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y;
i = 0x5f3759df - (i >> 1); // 这是什么鬼?
y = * ( float * ) &i;
y = y * ( threeHalfs - ( x2 * y * y ) );
return y;
}
后续有机会的话我会写篇文章研究一下 让人摸不到头脑的 0x5f3759df 的推导,有个叫 Chris Lomont 疯子(其实他是个数学家)不服,怒了,然后暴力方法找到了一个更好的数 0x5f375a86 ,呵呵了。
Python科学计算测试代码
这里先用Python科学计算的方法检验一下这个速算法的误差,在 IPython Notebook 中测试。
代码
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
number = np.linspace(0.1, 10, 100)
y = number.astype(np.float32)
x2 = y * 0.5
i = y.view(np.int32)
i[:] = 0x5f3759df - (i >> 1)
y = y * (1.5 - x2 * y * y)
y_s = 1 / np.sqrt(number)
error = y_s - y
np.max(np.abs(error))
plt.figure(figsize=(8, 4))
plt.plot(number, y, label = "$Fast\ Inverse\ Square\ Root$")
plt.plot(number, y_s, "--", label = "$Standard\ Inverse\ Square\ Root$")
plt.xlabel("Number")
plt.ylabel("Inverse Square Root Value Of Number")
plt.title("Inverse Square Root")
plt.legend()
plt.show()
plt.plot(number, error)
plt.xlabel("Number")
plt.ylabel("The Error Of The two Methods")
plt.title("The Error")
plt.show()
结果
两种方法得到曲线如下:
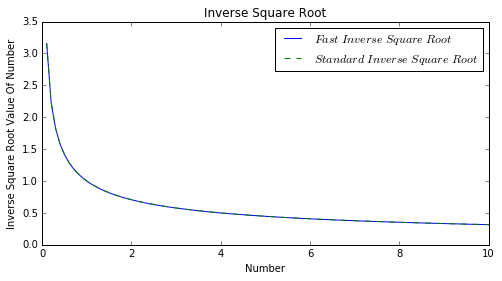
偏差曲线如下:
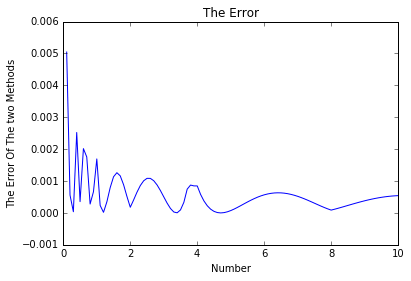
可以得到最大误差和最小误差:
np.max(error), np.min(error)
得到结果如下:
- (0.0050456140410597428, -4.9357368359093101e-08)
可以看到误差还是很微小的,所以当对速度要求高并且数据不需太精确时,用这个速算法比较合适。
v1.5.2